B+tree indexes

While there are other index types available, to add an index usually means to add a B+tree index, whether it be a primary key, unique or non-unique. By understanding B+trees well, you cannot just improve the performance of individual queries, but also reduce the amount of your data that must be in memory (the working set). This, in turn, helps improve the overall scalability of your database.

To explain how B+trees work I like to start with an explanation of how a binary tree works and then describe how they differ:

The main property of a binary tree is that it has binary search. This means that to find the value 829813 in a (balanced) binary tree of 1 million items it should take no more than 20 hops. This is a considerable improvement over scanning 1 million entries in a list:

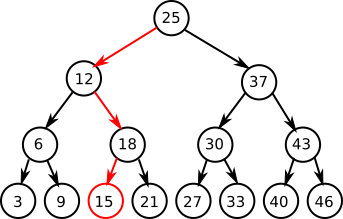
Where I would say a Binary tree is limited, is that 20 hops is actually a high number if it also results in 20 disk accesses. It also does not mitigate that very small IO accesses are relatively expensive [1] . By comparison, here is the same search in a B+tree [2] which uses only 2 hops:

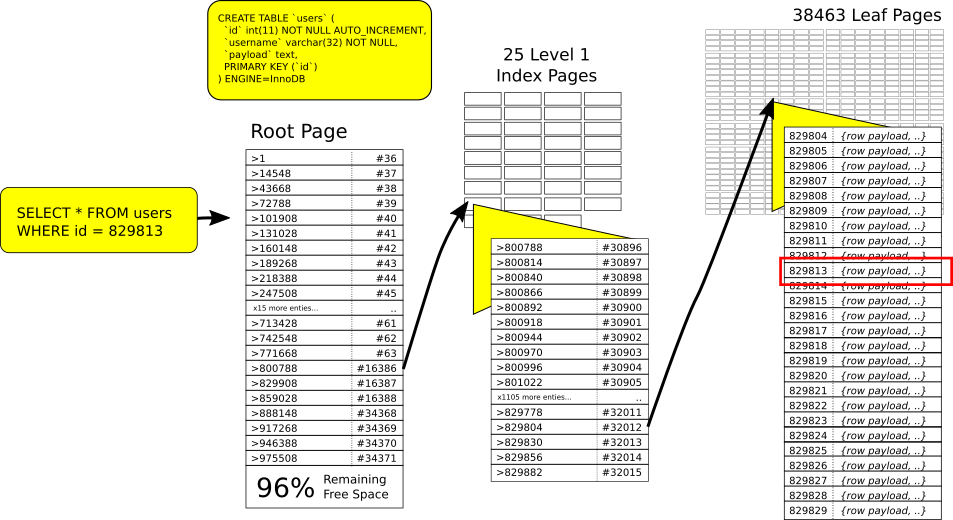
The above diagram shows that the root index page points to 25 different index pages, which themselves point to on average 1538 leaf pages. The path to row 829813 is highlighted:

• From the root page: values >= 800788 but < 829908 are on page 16386.
• From page 16386: values >= 829804 but < 829830 are on leaf page 32012.

So what we have in a B+tree are two specific enhancements over a binary tree:

1. There is an organization of data into pages. This is the basic unit of data that is organized together for reading and writing from storage. The organization in database terminology is called clustering (not to be confused with a database cluster).
2. The tree itself is wide and not deep. When you can fit 1000+ keys per index page, which can each point to another index page with another 1000 keys, it is uncommon to have a B+tree that is more than 3 levels deep in structure before the leaf pages (which for the primary key will contain the full row). Another way to phrase this is that the B+tree fans out much more quickly than the binary tree.

Keeping the root page plus 25 internal index pages in memory only requires 400KiB of memory (pages are 16KiB each). The 38463 leaf pages will require 600MiB for storage, but do not necessarily have to all be in memory at once. Most data sets have some pages that are hot, and others that are untouched. Internally InnoDB is keeping track of page access using a modified LRU algorithm [3] , and will evict the less frequently accessed pages if it needs to make room.

It is usually possible to have a total data size far exceed RAM. We refer to the portion of the data that needs to be kept in memory as the working set. Every data set has different working set requirements, and the goal of the database administrator is to find optimizations that can reduce it.

A 500GB database with a 300GB working set requirement is often much harder to optimize than a 1TB database with a 100GB working set.

[1]	It is usually a similar cost to read 4K as 500B. A B+tree helps amortize IO cost (true even for SSDs).

[2]	Showing the actual values from an InnoDB B+tree analyzed using https://github.com/jeremycole/innodb_ruby

[3]	https://dev.mysql.com/doc/refman/5.7/en/innodb-buffer-pool.html#innodb-buffer-pool-lru